Определение угла наклона акселерометром

скачать в pdf

Определение угла наклона различных объектов относительно гравитационного поля земли осуществляется прибором под названием инклинометр. Существует несколько физических принципов, на основе которых может быть создан инклинометр. Чаще всего наклон определяют с помощью силы гравитации Земли, геомагнитного поля, гироскопического эффекта или применяют косвенные измерения. Любой из перечисленных принципов имеет свои плюсы и минусы.

Проанализируем определение угла наклона с помощью силы гравитации Земли. Если единственной силой, действующей на объект является сила гравитации, то в этом случае для определения статичного угла наклона может быть использован MEMS-акселерометр (например, LIS3LV02DL), прибор, который измеряет проекцию ускорения (суперпозицию собственного ускорения акселерометра и вектора гравитации) на его чувствительную ось. По величине измеренной проекции определяется угол наклона.

На практике чаще всего на объект помимо силы гравитации действуют еще и другие силы, вызванные вращением, тряской и т.д. Так как сила гравитации имеет постоянную величину любые дополнительные силы, действующие на объект, изменят выходные данные акселерометра, а следовательно в расчете угла наклона появится ошибка. Применив предварительную обработку выходного сигнала акселерометра, можно свести влияние других сил к минимуму, но это приведет к задержке выдачи актуального значения угла.

Одноосевой акселерометр

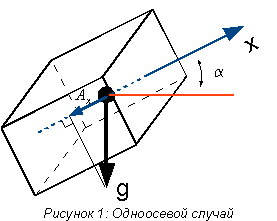Для начала рассмотрим идеальный случай, в котором ось X объекта всегда находится в плоскости действия силы гравитации. Воспользовавшись школьным курсом элементарной тригонометрии, получим выражение для вычисления проекции силы гравитации на ось Х:

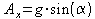(1)

где - угол между осью акселерометра и горизонтом. Обычно за горизонт принимают плоскость, ортогональную силе гравитации (Рисунок 1). Из-за того что выходное значение акселерометра пропорционально синусу угла наклона в поле гравитации, для определения угла наклона получим формулу:

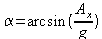(2)

Изучим характер зависимости проекции от угла наклона. По определению чувствительность инклинометра выражается отношением изменения его выходного сигнала к связанному с этим изменению угла. В одноосевом случае, если угол наклона близок к значению 90º, большое изменение угла приводит к маленькому изменению измеряемого ускорения. Таким образом, чувствительность измерения угла наклона будет стремиться к нулю с приближением значения угла к 90º.

Важной характеристикой инклинометра является величина его порога чувствительности. Эта характеристика определяет минимальную разность между двумя углами, которую прибор может измерить. Порог чувствительности акселерометра есть постоянная величина, значит для инклинометра он должен меняться подобно его чувствительности: наилучшее значение в районе угла наклона 0º и наихудшее при 90º.

Как подобрать акселерометр, который позволит нам получить желаемый порог чувствительности инклинометра на заданном интервале измеряемых углов? Акселерометр должен определить величину, на которую меняется проекция силы гравитации при изменении наклона на угол равный порогу чувствительности инклинометра. Разность двух показаний акселерометра при смене угла наклона представляется формулой:

(3)

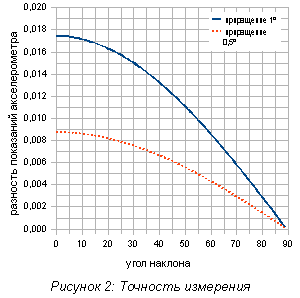
где - текущий угол, а - шаг приращения угла. Построим зависимость разности от угла наклона и величины приращения (Рисунок 2). Построенные кривые могут быть в дальнейшем использованы для определения минимального необходимого разрешения акселерометра, достаточного для того чтобы получить заданный порог чувствительности. По графику видно, например, для того чтобы получить порог чувствительности равным в 0.5º на диапазоне измеряемых углов ±55º, необходимо выбрать акселерометр с разрешающей способностью как минимум 5мg/LSB.

Достижение высокой разрешающей способности на широком диапазоне измерений, в одноосевом случае, возможно лишь с применением акселерометра обладающего высокой разрешающей способностью. Кроме того, такая схема не может работать в полном диапазоне углов 0º-360º так как значения синуса совпадают для углов Nº и 180º-Nº.

Двухосевой акселерометр

Избавиться от перечисленных недостатков поможет введение в систему измерения дополнительной оси чувствительности y, ортогональной оси x и также находящейся в плоскости действия силы гравитации (Рисунок 3).

Подобно ситуации с одним сенсором, значение ускорения измеренное акселерометром по оси X будет пропорционально синусу угла наклона, а значение ускорения измеренное акселерометром по оси Y– косинусу угла наклона. Из свойств функций синуса и косинуса следует, что в то время как чувствительность по одной оси будет уменьшаться, она же по другой будет увеличиваться. Расчет угла наклона можно провести воспользовавшись следующей формулой:

(4),
(5)

В отличие от одноосевого случая, применение отношения проекций для вычисления угла наклона, делает аналитическое определение порога чувствительности непростой задачей. Учитывая что чувствительность по одной оси растет в то время как по другой она падает, можно грубо считать общую чувствительность постоянной величиной. Такое поведение характеристики значительно упрощает выбор акселерометра, обладающего необходимой разрешающей способностью. Расчет порога чувствительности, выполненный для одного угла, будет справедлив для всего интервала измеряемых углов.

Любой наклон не по оси чувствительности приведет к значительным ошибкам измерения угла наклона одноосевым акселерометром. Введение дополнительной оси чувствительности позволяет получить довольно точные результаты, даже если присутствует наклон по третьей оси. Так происходит благодаря тому, что эффективная чувствительность инклинометра пропорциональна квадратному корню из суммы квадратов проекций силы гравитации на чувствительные оси.

Когда сила гравитации действует только в плоскости XY значение ускорения, которое измерит акселерометр, будет строго равно 1g. Наклон в плоскости XZ или YZ уменьшит измеряемое ускорение, что в свою очередь снизит чувствительность инклинометра. Но несмотря на это, все еще можно получить точные результаты, относящиеся к углу наклона в плоскости XY. Эти рассуждения справедливы только для не больших углов наклона в плоскости XZ и YZ. С ростом угла наклона влияние силы гравитации на оси X и Y будет уменьшаться, в итоге невозможно будет вообще рассчитать угол наклона.

Кроме того, дополнительная ось дает нам возможность измерять углы в диапазоне 0-360 градусов. Достигается это благодаря смене знака в зависимости от принадлежности угла к тому или иному квадранту.

Принадлежность угла к тому или иному квадранту, может быть определена в результате анализа значений, полученных для каждой из чувствительных осей.

Трехосевой акселерометр

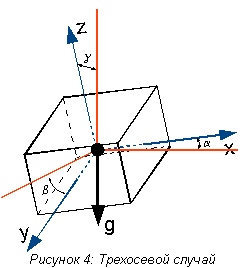Введение третьей чувствительной оси позволит измерять все углы наклона сенсора в пространстве. В начальной позиции положение устройства такое, при котором оси x и y находятся в плоскости горизонта, а ось z ортогональна осям x и y (Рисунок 4).

В начальной позиции, когда сила гравитации действует только на ось z, получим, что все значения углов равны 0. При этом, значения углов могут быть вычислены по следующим формулам:

(6)
(7)
(8)

Как и в 2-х осевом варианте, порог чувствительности постоянен и это позволяет точно измерить значения углов для всей сферы.

Калибровка акселерометра

Приведенные выше рассуждения для всех трех вариантов сенсора, выполнены с предположением о том, что используется идеальный акселерометр. А значит, он обладает идеальной чувствительностью и у него отсутствует какое-либо смещение нуля. В реальности же MEMS-акселерометр представляет собой механическое устройство и, несмотря на то, что он отрегулирован, после установки его в инклинометр, на него будет действовать статичная «нагрузка». В свою очередь это приведет к изменению чувствительности и смещению уровня нуля инклинометра. Как результат инклинометр будет выдавать значения углов наклона с точностью значительно хуже заданной. Снизить ошибку определения угла наклона поможет калибровка нулевого значения акселерометра и его чувствительности.

Для калибровки акселерометра можно избежать применения дорогостоящего оборудования. Достаточно снять несколько показаний акселерометра, в случае если на него действует только сила тяжести.

С учетом начального смещения и чувствительности сенсора, все получаемые значения от акселерометра можно представить в таком виде:

(9)

где - начальное смещение; K – коэффициент чувствительности; 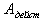- действительное значение ускорения, действующего на сенсор, равно 1g; - угол между действующим ускорением и чувствительной осью сенсора. Задача начальной калибровки сводится к нахождению величин и K. Для нахождения указанных величин, снимем показания с акселерометра, в положениях, когда ось чувствительности последовательно повернута на угол 0º, 90º, 180º и 270º относительно начального. Математически полученные значения можно записать в такой форме:

(10)
(11)
(12)

Учитывая что , а , после сложения выражений (9), (10), (11) и (12) получим:

(13)

Для нахождения коэффициента чувствительности воспользуемся следующими тригонометрическими тождествами: и .

Записав сумму квадратов разностей и получим что:

,

откуда:

(14)

Рассмотренный способ калибровки акселерометра не требователен к начальной ориентации оси чувствительности, что значительно упрощает его выполнение. Описанную последовательность действий необходимо провести для каждой из осей чувствительности акселерометра.

Литература

1. Using an Accelerometer for Inclination Sensing by Christopher J.Fisher. (AN-1057.pdf)
2. http://ru.wikipedia.org/wiki/Клинометр
3. http://ru.wikipedia.org/wiki/Чувствительность_(техника)